
Actually, reversing it is the main reason I have it.
Korg released the ES-1 in 2000 and describes it as a “rhythm production sampler”. It’s relevant today as a piece of cheap used hardware that’s easy and fun to use.
And not only for making music!

Actually, reversing it is the main reason I have it.
I’ve taken a technical interest in samplers since the time I became aware of their creative use in the production of late 1990’s drum & bass. I dreamt of my own product ideas and wanted to better understand how samplers are designed. In that respect, the ES-1 would only be a rough guide, because technology is much different today. Nevertheless, I felt the ES-1 offered me a lesson.
I guess most people learn reverse engineering through practice, not training. Most of the literature I have encountered on reverse engineering aims at software that runs on an operating system. Tricks that work in that context won’t work for an embedded system like the ES-1, where we’d struggle to access its software as data.
When you reverse engineer something, some of your questions will go unanswered. The usual goal of reverse engineering is not to fully understand a system, but to understand it enough that you can move toward some other goal.
The ES-1 comes apart with a screwdriver and gentle force. You can identify its main parts and get their datasheets.

I couldn’t find a datasheet for the DSP. According to hearsay on the web, the part was sold only in Japan, was not released to the public, and Texas Instruments in the USA knows nothing about it.
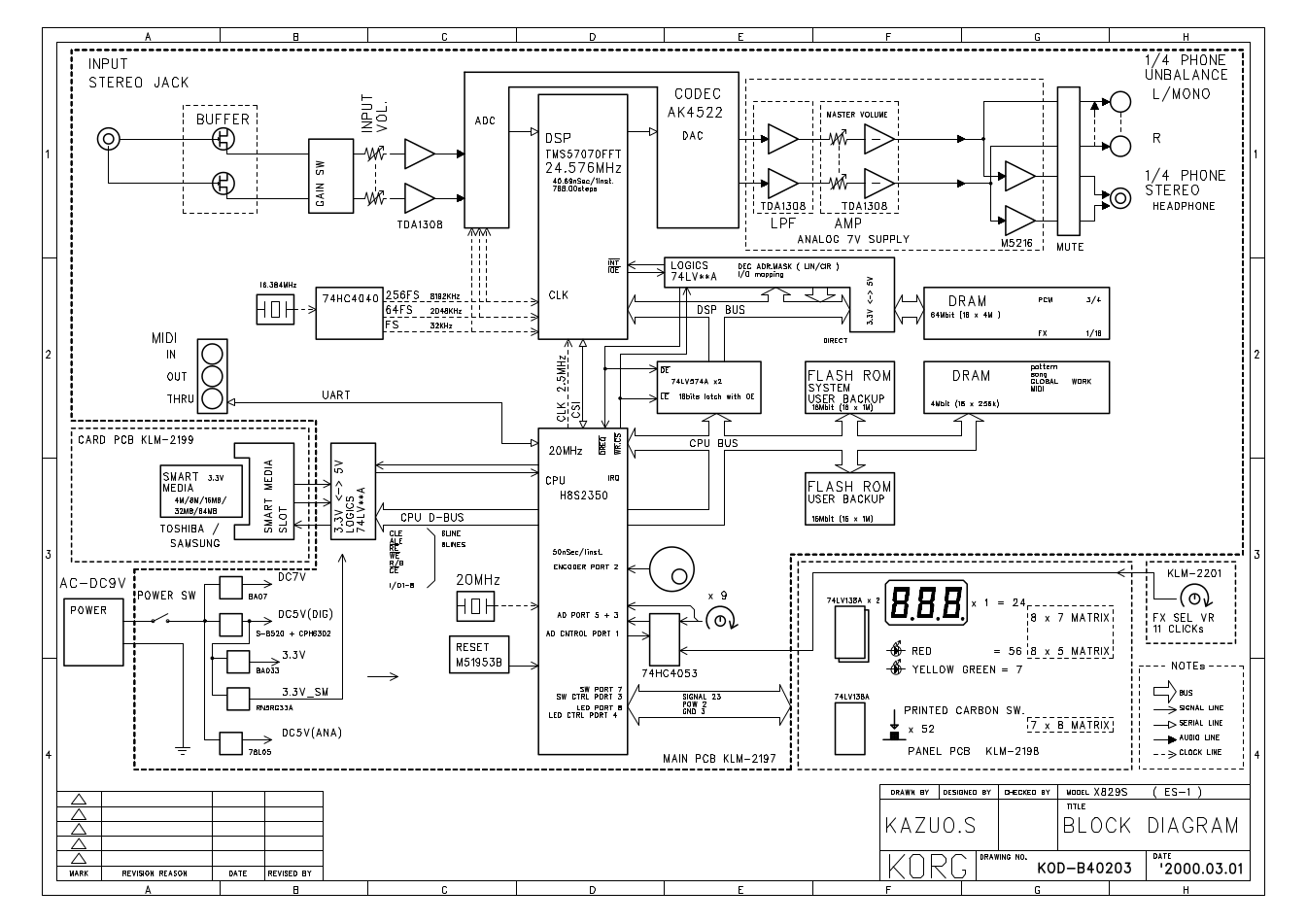
The service manual has a helpful block diagram of the overall hardware design.
After tinkering with the ES-1, I took interest in the backup files. The ES-1 uses a SmartMedia card to save all of its data. The files it saves are not understood by anything else—except Korg’s Windows-only “ES-1 to .WAV PC Utility.”
Undocumented data formats annoy me as much as companies who fail to publish cross-platform utilities. I believe it is virtuous to document such formats and make them more useful. Plus, hacking a file format gave me an offbeat introduction to reverse engineering, and I have a soft place in my heart for offbeat introductions. I had learned, from troubleshooting hosted software, that data almost never gives clear evidence of functionality. It’s much easier to understand a system by observing its logic, if you can. Embedded systems often make that hard. But the Windows-only utility, under the right conditions, might help.
Here’s a diagram of what data and interfaces are easily accessed.
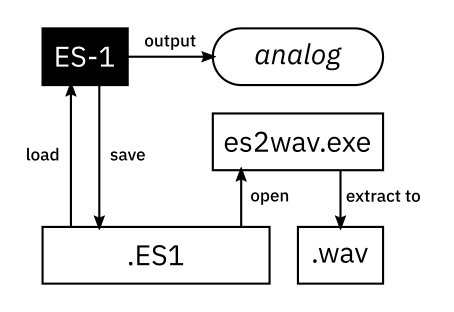
Even if we don’t observe the internals of the ES-1, there are plenty of other things to observe.
We can
The PC Utility is interesting because it contains a decoder for the backup format. Although I don’t use Windows, it’s possible to run many Windows programs on Linux using Wine. However, Korg’s terms of service seemed to discourage reverse engineering, so I avoided that. (Only to return to it later!)
As I tinkered, I realized that the encoding of the stored audio wasn’t obvious. I considered a few ways to reverse it:
Identify a relationship between .ES1 files and the analog output signal. Being downstream of the decoder, the analog signal could reveal only acoustic or graphical evidence of the encoding. But that doesn’t make it useless.
Identify a relationship between .ES1 files and the extracted .wav files. This can be done without disassembling es2wav.exe, making it clearly compliant with Korg’s terms of service. But it still provides only indirect evidence of the decoder.
Reverse es2wav.exe. Find the decoder as expressed in machine code. I delayed this approach until I believed it was legally defensible.
I learned an important lesson from troubleshooting hosted software:
You can gain more understanding of a system by observing its logic than by observing its data.
The evidence of logic that you find in data is often unclear, unless the data is code. The backups are easy to access, but they might be hard to use. es2wav.exe implements a decoder, so it has to exhibit the logic we’re after. But I held off on reversing it because of legal concerns.
How far could I get without probing the hardware? I saved a backup. Maybe I’d be lucky.
$ file 1.ES1
1.ES1: data
No obvious file type. I looked inside.
$ r2 -c pxi 1.ES1
0 1 2 3 4 5 6 7 8 9 A B C D E F
0: .K .O .R .G 01 .W 02 bb b3
10: .E .E .E .E .E .E .E .E .E ./ .6
The magic number is “KORG”. The number occurs once more in the backup.
[0x00080000]> pxi
0 1 2 3 4 5 6 7 8 9 A B C D E F
80000: .K .O .R .G 01 .W 01 af .>
80010: .> .c . .N .b ## 10 .> .b ##
I inspected several different backups, some of which had no audio samples. All of them were 3.7 megabytes in size; 29 × 2¹⁷ bytes. The constant size, just under a round number, suggested a binary image dump. I wanted to understand the hardware that would be storing the image.
I took apart the ES-1 with a screwdriver and a little force. Inside, I found two flash memory chips.

Fujitsu 29F160BE-70PFTN.
The service manual labels one flash chip “system.” Does it store code?
Together, they are four megabytes; just big enough to store a backup. I guessed that the backups were near-copies of the flash memory. But that would be hard to disprove without probing the hardware.
I also wondered if the “KORG” magic numbers could mark sections of the file that go on different chips. That’s easy to disprove, by observing one of the sections to be bigger than two megabytes. Since the second “KORG” appeared at 0x80000 (about half a megabyte), it meant the second section would be too big to fit on a 2-megabyte flash chip.
The ES-1 supports loading 8- and 16-bit linear PCM samples. I guessed that it encodes them directly1. To test this, I saved a backup as a reference point. I wrote a C program to make PCM data with a clear pattern when displayed in hexadecimal.
int16_t frames[1<<10];
for (size_t i = 0; i < len(frames); i++)
frames[i] = i < 128 ? INT16_MAX : 0;
fwrite(frames, sizeof(frames[0]), len(frames), stdout);
This makes 128 frames of 0x7fff followed by zeroes; a pulse. I built the program and the WAV file
$ make main && ./main | ffmpeg -i /dev/stdin -f s16le \
-ar 32000 -ac 1 -y /media/karl/disk/00.wav
and loaded it. I saved another backup and used dhex to view the difference between the two backups.
$ dhex /media/karl/disk/*.ES1
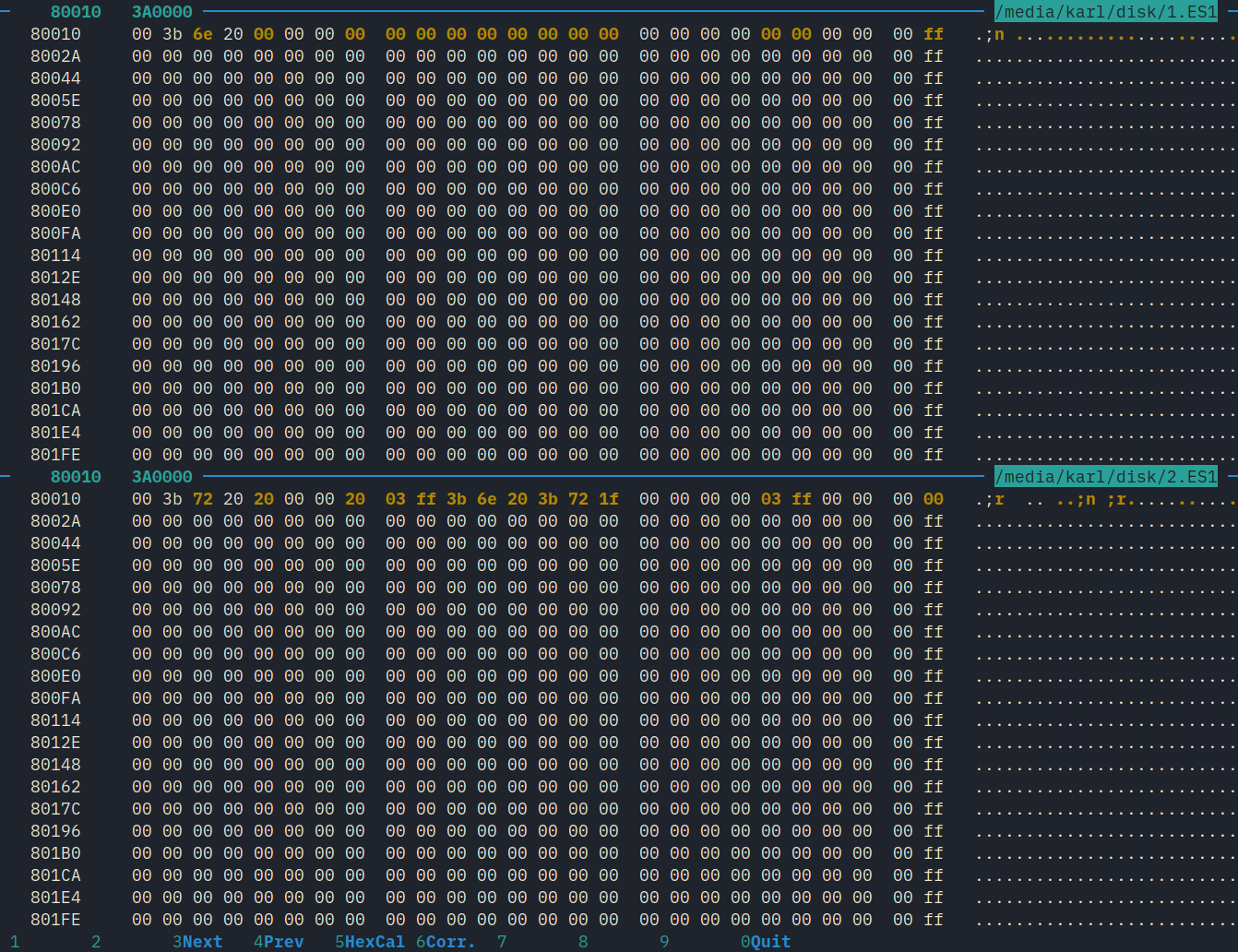
In an unknown data structure, a few bytes have changed. Oddly, this change appears a second time elsewhere in the backup.
Several parts of the backup had changed. The string “03ff” appeared a few times. After testing again with audio samples of different lengths, I found that this number is always one less than the number of audio frames. It occurs in what I guess is a data structure that manages how the samples are stored.
Further down in the backup, a big chunk had changed. It seemed like audio data.
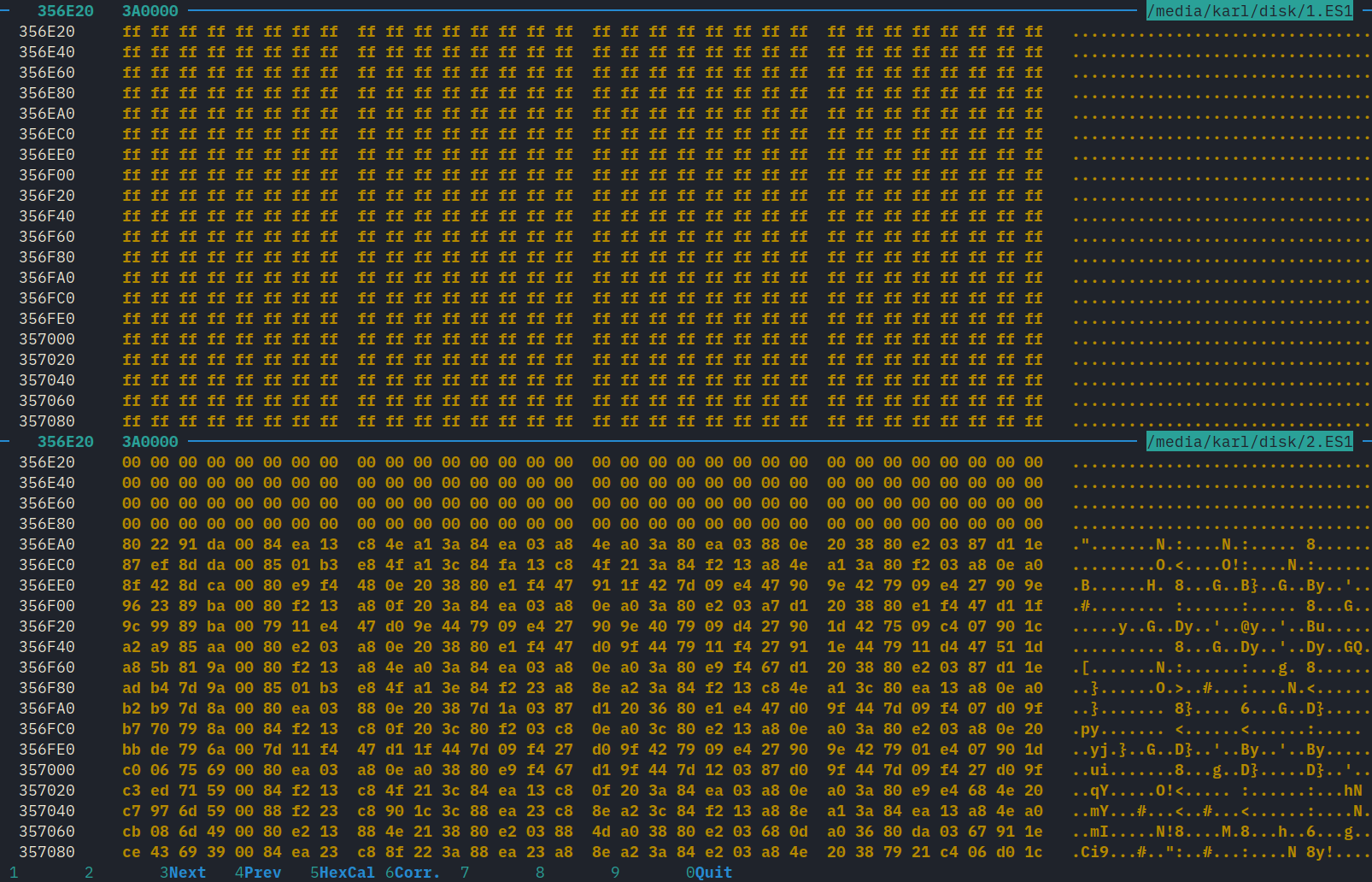
Free space, shown in the top window, sometimes had arbitrary data. The 0xFF values shown here may be from erasing sectors of the flash memory.
The chunk didn’t have the expected values. Therefore, PCM isn’t the encoding it uses. But it looked promising! It began with a long string of zeroes. There are 32 × 4 = 128 zeroes, which is exactly the number of non-zero frames in the impulse! But the zeroes are followed by a long, complex string that I couldn’t explain.
I tested again with many different samples. I wanted to see how the encoding would handle extreme inputs:
I also played the samples back on the ES-1 and observed with an oscilloscope, and listened to them.
Low-frequency, full-scale square waves proved a very effective test.
By starting each time with the same backup image—which had no
samples—I found that the chunk would always be at the same place in the
file: 0x356e20.
However, a later experiment showed this address was incidental:
I loaded the backup image and let the ES-1 record digital silence until it ran out of memory. This filled a large area of the backup with zeroes, revealing the location and size of the audio storage. After I deleted the long sample, the zeroes remained. But after that, new samples were written to a different location: 0xa0000. So I found that the audio is stored from 0xa0000 until 0x3a0000, which is the end of the file.
I realized that the backups contain some state that isn’t functionally relevant. Backups that are not byte-for-byte identical can still contain the same application data. The differences, I guessed, had to do with the state of the ES-1’s free space and associated management structures2.
The ES-1 apparently doesn’t defragment free space when samples are deleted. Instead, it defragments when samples are written. That agrees with my experience using the ES-1: writing a sample sometimes takes very long. The user manual even warns about it!

Reverse engineering tip #0: read the manual.
The length of the chunk changes monotonically and roughly linearly with the length of the sample. The data in the frames does not affect the length of the chunk. Because of this relationship, I guessed that the ES-1 doesn’t use general-purpose data compression, such as Huffman coding. Data compression would show a non-monotonic relationship that depends on the data in frames.
I observed how the encoding reacts to small differences in frame data. This led me to observe a dimensional correlation: changes at one point in the audio file cause changes in a roughly similar area of the chunk.
I saw that the length of the chunk is approximately, and sometimes exactly, half the size of the PCM data.
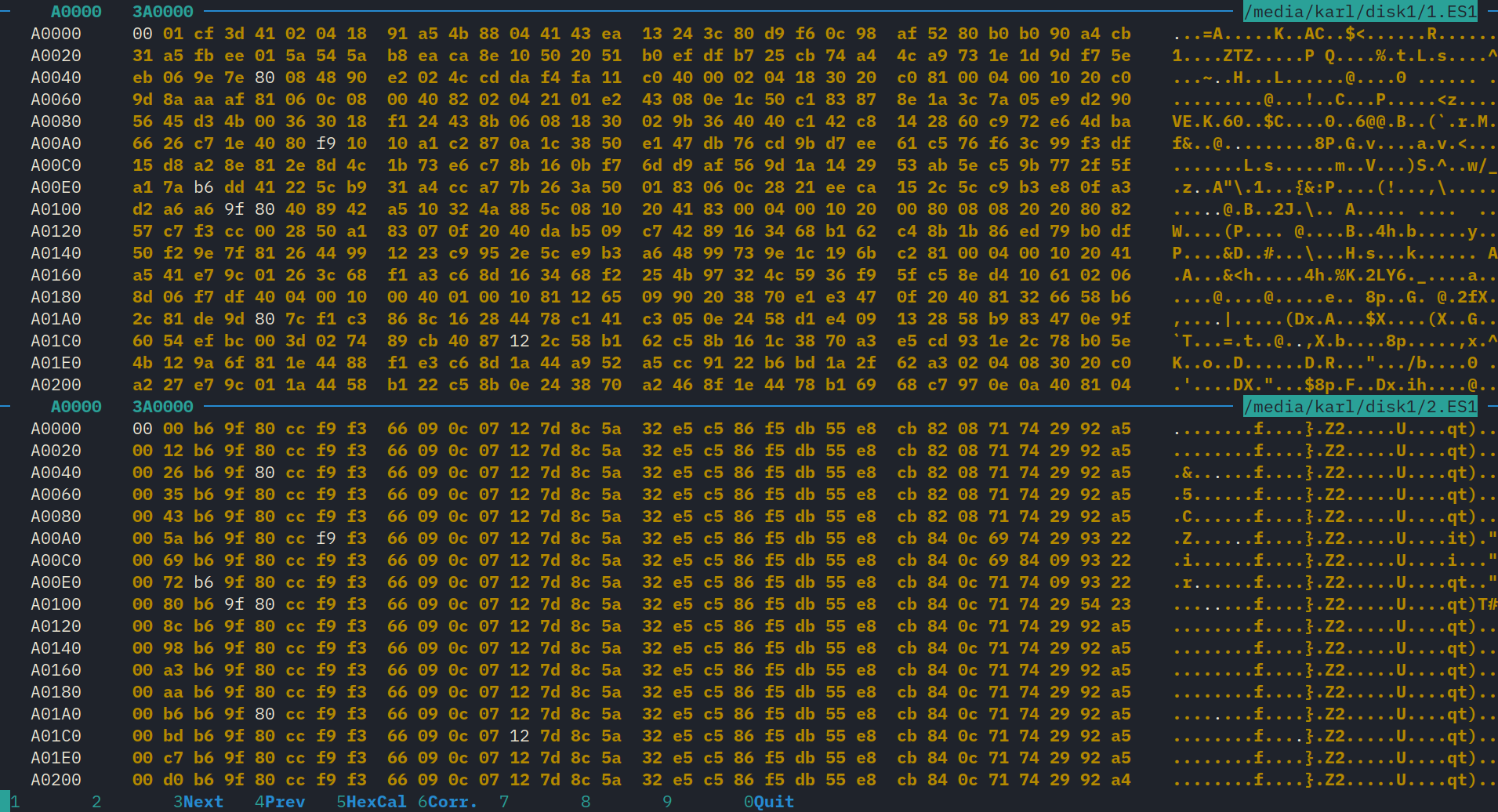
By using periodic waveforms, such as a 1kHz sine wave, there was a clear 32-byte regularity. It wasn’t perfect, however, which was hard to explain. The chunks seemed to be made of 32-byte blocks. A change to the first frame would often be spread out over the first 32-bytes.
The sample rate is 32kHz. So my next guess was that each 32-byte block encodes 1ms of audio, with one byte per frame.
This seems like a hash function from a 64-byte, 1-ms chunk of audio to a 32-byte block. The hash function exhibits poor avalanching, which I would expect in a non-cryptographic application.
Reversing a hash is hard unless you can observe a pattern.
The encoding produced unexpected results for several inputs. You have two ways to observe the output of the decoder:
Play the samples back on the ES-1 and observe the output signals. You can see the signals using an oscilloscope, or record them into your computer.
Use the ES1-to-WAV utility program distributed by Korg. This program extracts WAV samples from a .ES1 file. This software is distributed under a license which forbids reverse engineering “unless permitted by law.”
As to the fact that a 1kHz waveform isn’t encoded as identical blocks? The ES-1 does some processing to samples before they are loaded.
First, it assumes that the value of the first frame is the DC offset of the entire sample, and subtracts it from every frame. If your sample doesn’t start at zero, then it gets shifted. This can actually increase the DC offset.
Then! as if to realize that this is the wrong way to remove DC offset, it applies a causal highpass filter, which creates phase distortion at low frequencies.
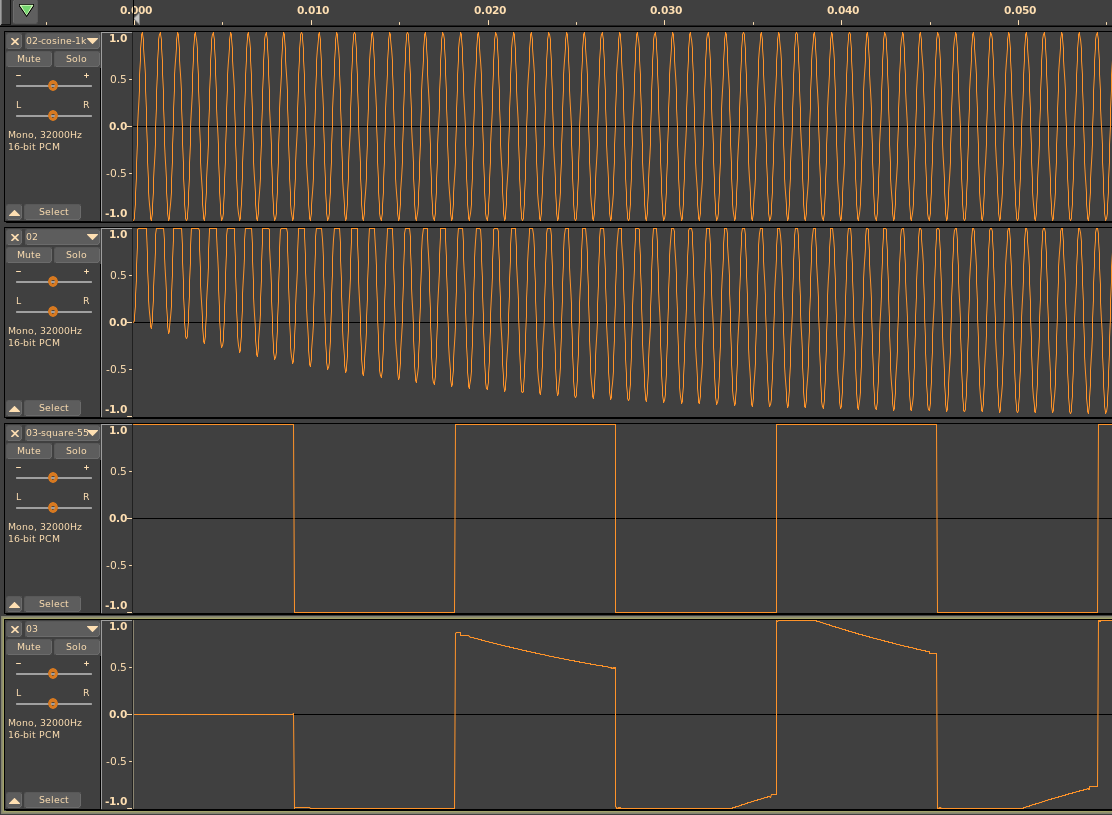
The result? The phase distortion can cause clipping artifacts for high-amplitude, low-frequency samples. And if you want to play impulses, say, for capturing delay and reverb effects, they have to be delayed by at least one sample, otherwise the preprocessing turns them into exponential decays!
It seems that Korg was concerned that users would load samples with DC offset. I don’t know why they didn’t remove the offset the correct way: subtract the average frame value from each frame. This does not add phase distortion. It could still cause clipping, however, if the sample isn’t renormalized.
Because of the preprocessing, you can’t directly access the input to the encoder. But, you have backups; you can directly access the output of the encoder; and therefore, you can directly access the input of the decoder.
load write
_______
*.wav → [preprocessor] → [encoder] → | |
| *.ES1 |
analog audio ← [decoder] ← |_______|
play load all
You can modify the backups and load them. This is risky, because you don’t know if the decoder can safely process arbitrary data. To avoid the risk of bricking the ES-1, I opted to take an existing, valid 32-byte block and repeat it for the remainder of the sample. Then observe the sample when it is played back. Since you aren’t observing the direct output of the decoder, you can’t come to a firm conclusion. But this will rule out the possibility that the variation between blocks is because of chaining.
And indeed, it seems to be true. Repeated blocks yield 1kHz periodic waveforms.
Next, I filled the chunk with random data. This never bricked the ES-1, so I guess I was lucky.
This technique targeted the decoder. The waveforms crackled and popped intermittently. (I felt satisfied, as I hadn’t expected Beethoven to come out.) There were many periods of silence interrupted by pops, topped with jagged edges, that were synchronized with a 1kHz clock. I wondered if the silence was the result of invalid data. The 1kHz synchronization seemed to fully confirm the idea that the encoding works in 1ms, 32-frame units.
The random data helped to see overall patterns, but it sucked to identify fine details. Moreover, the approach had become tedious. Each load and save takes about 30 seconds, so I’d waited long to learn all of this. I wanted a more efficient technique.
I reconsidered the PC Utility. I realized that as long as I restricted my observation to input and output, I was not running afoul of the terms of use. My new approach was to synthesize backups and let the PC Utility generate audio files. This was still pretty slow because the PC Utility requires mouse interaction, and is difficult to automate.
Synthesizing data allowed me to test the block format systematically. Each block could have one of 340282366920938463463374607431768211456 values, and I wasn’t going to test them exhaustively. There seemed to be regularity at the beginning of each block, so I started with the first byte.
It turned out that the first two bytes encode the DC offset. Other than that, the encoding is not straightforward.
I read the PC Utility’s terms of service carefully. There’s an exception for reverse engineering if it is “permitted by law.” Let’s figure this out.
The Electronic Frontier Foundation (EFF) publishes an FAQ about the legality of reverse engineering. Reading it did not resolve my doubt, so I asked the EFF for help. They referred me to three different attorneys. One of them kindly gave me a useful summary, which I’ve put into my own words:
In copyright law, creative expression can be copyrighted, but functionality cannot.
A unit of code mixes creative and functional elements.
A copyright owner cannot use a license to limit access to functional parts of software.
Since reverse engineering is the only way to glean the functionality of software from its expression, a copyright owner cannot forbid others to reverse the software to get the functional elements. That is “fair use,” which is a defense to copyright infringement.
Reverse engineering is fair use if done for a legitimate reason, such as to make an interoperable product. An example of an illegitimate reason is distributing copyrighted material (expressive elements) with or without modifications.
It seemed that my project was defensible if I avoided distributing Korg’s “expression.”
I knew the decoder would run between reading the backup and writing the output files. I guessed it was contained in the 100-kB es2wav object identified by winedbg:
$ winedbg es2wav.exe
Wine-dbg>info share
Module Address Debug info Name (24 modules)
PE 400000- 419000 Deferred es2wav
PE 630000- 87c000 Deferred comdlg32
PE 880000- d25000 Deferred comctl32
I explored options for detecting the read and write events.
Win32 API calls:
$ WINEDEBUG=+relay wine es2wav.exe 2>log.txt
$ grep -in '00\.wav\|payload' log.txt | grep -i create
928225:0110:Call KERNEL32.CreateFileA(00412ce0 "Z:\\home\\karl\\source\\scratch\\es-1-reversing\\payload.ES1",80000000,00000003,01d1fe30,00000003,00000080,00000000) ret=00408b9d
1483032:0110:Call KERNEL32.CreateFileA(01d1fd88 "Z:\\home\\karl\\Desktop\\00.wav",80000000,00000003,01d1fd1c,00000003,00000080,00000000) ret=00408b9d
1488958:0110:Call KERNEL32.CreateFileA(01d1fd6c "Z:\\home\\karl\\Desktop\\00.wav",40000000,00000003,01d1fcf4,00000002,00000080,00000000) ret=00408b9d
The same PID (0x0110) was used for each of these calls.
Linux system calls:
$ strace -i -f -o es2wav.strace wine es2wav.exe
Later on, I had much more success with static analysis than dynamic. Radare visual mode was extremely helpful in tracking down control flow and finding interesting bits of code.
I felt silly when I found a block of code that pushed “KORG” onto the stack and handed it to a subroutine. That’s got to be the beginning of the input validation.
That led me to identifying many functions of the C standard library, which allowed me to track handles for input and output files. Eventually I found the core of the decoder. It’s extremely complex.
It was fun, although ended in more of a whimper than a bang. While I didn’t succeed in replicating es2wav’s functionality (and probably couldn’t have legally—instead I’d have to come up with a functional spec and hand it off to another team, cleanroom style) I found some sources of distortion that contribute to the ES-1’s sound.
I also learned a bit about the structure of Windows applications.
I never did figure out if the backups contain ES-1 firmware. It was a missed opportunity to have upgraded the firmware without doing a diff between backups. I would have looked for a version number change, at the least. But much more would have changed. Radare can disassemble H8/300 code, whereas the ES-1’s processor uses the H8S/2000 instruction set, which is a superset.
This guess could have been ruled out with some basic facts and unit analysis. The ES-1 stores at least 95 seconds of audio at 32kHz. With 16-bit samples, PCM encoding would take (2 bytes/sample) × (32000 samples/second) × 95 seconds ≅ 6 megabytes. The backups and flash memory are smaller than that, so the audio couldn’t be encoded as PCM. But ruling out a guess with different tests isn’t a waste of time. It can help you find wrong assumptions and make new observations. ↩︎
For an introduction to free-space management algorithms, read OSTEP Chapter 17. ↩︎
Discuss this page by emailing my public inbox. Please note the etiquette guidelines.
© 2025 Karl Schultheisz